Автоматическое построение геометрических иллюстраций из текста

Анализ подхода на основе семантических сетей и шаблонного анализа

Контекст: Магистерская диссертация 2009 года (АФТ УФ РАН, Санкт-Петербург) исследовала задачу автоматического построения иллюстраций к задачам по планиметрии. Данная статья критически рассматривает выбранные технические решения, их ограничения и актуальность.

Постановка задачи

Требуется: по текстовому описанию геометрической задачи на естественном языке (русском) построить корректную иллюстрацию.

Практическая мотивация: автоматизация создания иллюстраций для электронных учебников и задачников снижает трудоёмкость подготовки материалов и позволяет динамически генерировать изображения для разных вариантов условий.

Исследовательская мотивация: задача требует формализации процесса визуализации, что представляет интерес для изучения связи языка и пространственного мышления.

Декомпозиция задачи

Задача распадается на три независимых подзадачи, каждая из которых представляет самостоятельную область исследований:

Уровни обработки

Лингвистический анализ: токенизация, морфологический разбор, синтаксический парсинг предложений на естественном языке
Семантический анализ: построение промежуточного представления (семантической сети), отражающего объекты и отношения между ними
Геометрическое построение: определение порядка рисования и вычисление координат в двумерном пространстве

Критическое замечание: наиболее сложной оказывается третья подзадача, так как она требует формализации неявных эвристик, которые человек применяет интуитивно.

Проблема порядка построения

Центральная сложность — определение корректной последовательности рисования геометрических объектов.

Пример условия:

«В треугольнике ABC проведена медиана BM. Через точку M провели прямую, параллельную стороне AB.»

Граф зависимостей:

Треугольник ABC — первичный объект (нет зависимостей)
Точка M — зависит от AC (середина отрезка)
Медиана BM — зависит от B и M
Прямая через M — зависит от M и направления AB

Следствие: необходимо построить DAG (направленный ациклический граф) зависимостей и определить топологический порядок обхода. Циклические зависимости указывают на некорректность или недоопределённость условия.

Ограничения и инварианты

Проблема коллинеарности: если условие требует "прямая, проходящая через точки A, B, C", наивный подход (случайно сгенерировать три точки, затем построить прямую) приводит к вырожденному случаю.

Корректное решение:

Построить прямую как первичный объект
Разместить три точки на прямой как зависимые объекты

Обобщение: для любого геометрического ограничения необходимо явно учитывать зависимости между объектами. Система должна различать первичные (independent) и вторичные (dependent) объекты.

Архитектура решения: три кита

Проект разбивается на три большие части:

1. Построение семантической сети

Семантическая сеть — это граф, где узлы — понятия (точка, треугольник, прямая), а рёбра — связи между ними (принадлежит, перпендикулярен, является вершиной).

Чтобы построить её из текста, используется язык шаблонов:

Шаблон "ОБОЗНАЧЕНИЕ":

<геометрический объект> <метка>

Примеры: «треугольник ABC», «отрезок MH», «точка X»

Результат: создаётся связь «ABC обозначает треугольник»

Текст разбивается на предложения, слова сопоставляются с понятиями (например, «вершина», «ортоцентр» → тип point), затем применяются шаблоны для поиска связей.

2. Обработка семантической сети

Полученная напрямую из текста сеть ещё сырая. Нужна «нормализация»:

Декомпозиция: «четырёхугольник ABCD» разбивается на четыре точки A, B, C, D и связи между ними
Объединение: если встречается «отрезок AB» и «треугольник ABC», точка A — одна и та же!
Дедупликация: удаление избыточной информации

Этот этап соответствует «мышлению» — обдумыванию условия перед рисованием.

3. Построение иллюстрации

Теперь самое интересное — алгоритм рисования. Вот его логика (упрощённо):

Рисуем случайным образом самую большую фигуру (ту, которой принадлежит больше всего точек) — например, треугольник
Ищем точки, которые однозначно заданы уже нарисованным (например, середина стороны)
Рисуем фигуры, которые теперь можно построить по этим точкам (например, медиану)
Повторяем шаги 2-3, пока возможно
Если остались неопределённые точки, выбираем ту, у которой наименьшая степень свободы, и рисуем случайно (с учётом ограничений)
Повторяем, пока всё не нарисовано

Аналогия с кроссвордом: сначала заполняем самое длинное слово, потом используем пересечения, чтобы вписать остальные.

Технические хитрости

Классы фигур и конструкторы

Каждая геометрическая фигура — это класс с несколькими конструкторами, отражающими разные способы её построения:

Окружность можно задать:

Центром и радиусом
Центром и точкой на окружности
Тремя точками

Программа выбирает конструктор в зависимости от того, какие данные уже есть.

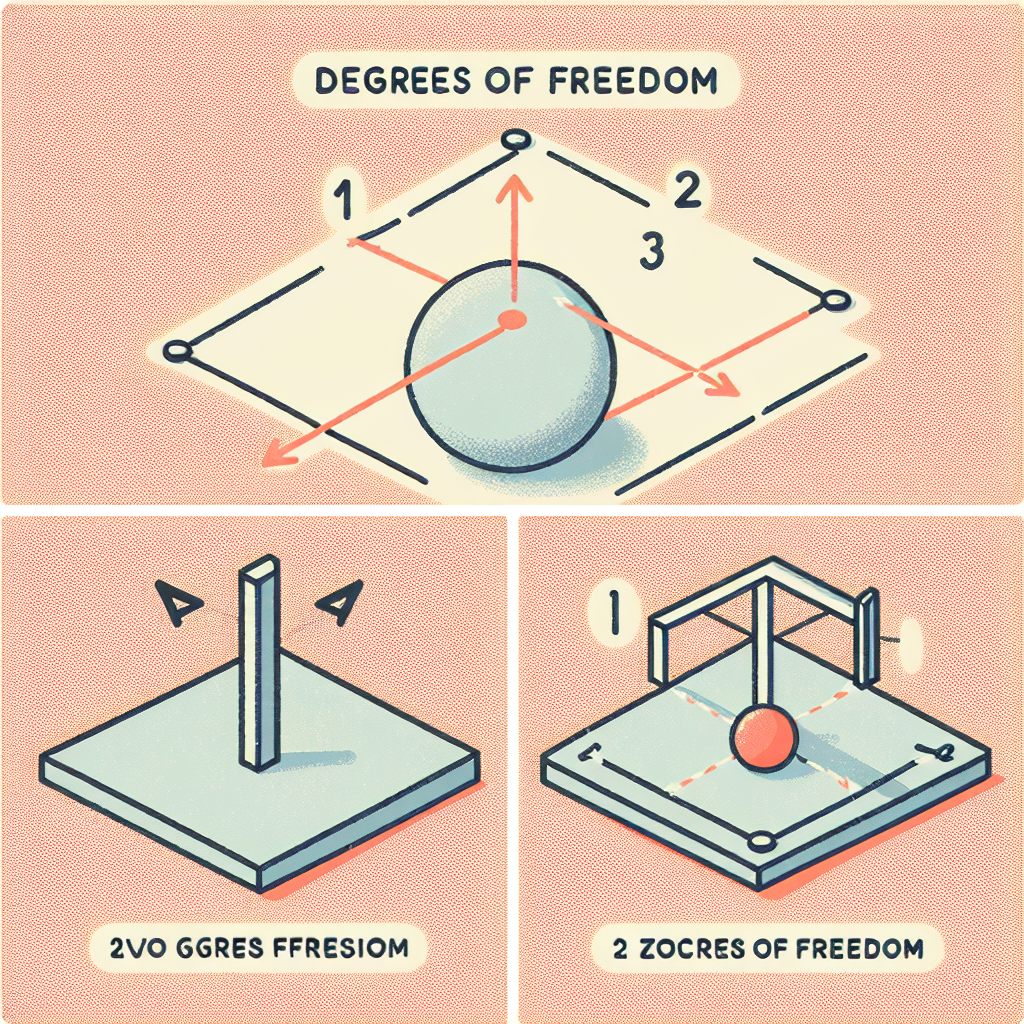
Степень свободы

Когда точка не задана однозначно, программа оценивает её степень свободы:

Точка на прямой — 1 степень (можно двигать вдоль прямой)
Точка на плоскости — 2 степени (x и y независимы)
Точка на пересечении двух прямых — 0 степеней (однозначно задана!)

Рисуем точки с минимальной степенью свободы — так меньше произвола.

Что это даёт нам сегодня?

Проект 2009 года, но идеи актуальны:

Для образования

Автоматические иллюстрации в электронных учебниках
Интерактивные задачники, где можно менять условие → картинка перерисовывается
Системы проверки: студент описывает конструкцию словами, программа проверяет корректность

Для исследований

Моделирование визуального мышления
Изучение связи между языком и пространственными представлениями
Тестирование подходов к семантическому анализу в узких доменах

Современный контекст

В 2009 году использовались шаблоны и графы. Сегодня, в эпоху больших языковых моделей:

ChatGPT / GPT-4 умеет генерировать код для рисования (SVG, TikZ) по текстовому описанию
Multimodal модели (GPT-4V, Gemini) могут анализировать диаграммы и генерировать их
Специализированные системы (например, на базе theorem provers) решают геометрические задачи формально

Но! Базовые принципы остаются: понимание зависимостей, порядок построения, степени свободы. Нейросеть может «понять» текст лучше, но логика геометрического построения — та же.

Детали реализации: как это работает на практике

Теперь перейдём к техническим деталям — как именно всё это было реализовано в коде.

Язык шаблонов для семантического анализа

Вместо полноценного NLP-парсера был разработан специализированный язык шаблонов. Это компромисс между простотой реализации и выразительностью.

Структура шаблона

Каждый шаблон состоит из двух частей:

Трафарет — правило поиска в тексте (регулярное выражение над типами понятий)
Заготовки связей — список связей, которые нужно создать для найденных понятий

Пример шаблона: ОБОЗНАЧЕНИЕ

Трафарет: <геометрический_объект> <обозначение>

Заготовка связи: обозначение.isSignOf(объект)

Найдёт: "отрезок MH", "точка X", "треугольник ABC"

Создаст: узлы для отрезка и обозначения "MH", связь между ними

Пример сложного шаблона: ПЕРПЕНДИКУЛЯР

Трафарет: прямую <sign1>, перпендикулярную <geom2> <sign2>

Заготовки:

sign1.isSignOf(line1) — первая прямая
sign2.isSignOf(geom2) — второй объект
line1.isPerpedicularTo(geom2) — отношение перпендикулярности

Найдёт: "прямую l, перпендикулярную отрезку AB"

Этапы обработки текста

Токенизация: текст → предложения → слова. Каждое слово становится объектом со ссылками на соседей
Морфологический анализ: выделение основ слов ("вершина", "вершины", "вершине" → одна основа)
Сопоставление типов: "точка", "вершина", "ортоцентр" → тип point
Применение шаблонов: к каждому предложению применяются все шаблоны связей

Преобразование текста в "помеченную" последовательность:

Пример преобразования

Исходный текст:
"Через H провели прямую, перпендикулярную отрезку MH, которая пересекла прямые AB и BC в точках X и Y."

После маркировки типов:
Через H-sign провели прямую-line, перпендикулярную отрезку-piece MH-sign, которая пересекла прямые-line AB-sign и BC-sign в точках-point X-sign и Y-sign.

Найденные понятия:

H (обозначение)
прямая (тип: line)
отрезок MH (piece + обозначение)
прямые AB, BC (line + обозначения)
точки X, Y (point + обозначения)

Математическая модель семантической сети

Семантическая сеть формализована как ориентированный граф:

Формальное определение

Множество типов узлов:
NodeTypes = {sign, point, line, piece, triangle, square, circle, ...}

Множество типов связей:
LinkTypes = {isSignOf, belong, isVertex, isCenter, isPerpendicular, ...}

Узел: node := (id, nodeType), где id ∈ ℕ₀

Связь: link := (node₁, node₂, linkType)

Сеть: S := ({nodes}, {links})

Нормализация сети: декомпозиция и синтез

Самая хитрая часть — превратить "сырую" сеть в удобную для рисования. Это трёхэтапный процесс:

Этап 1: Декомпозиция (разложение на атомы)

Сложные понятия разбиваются на простейшие составляющие.

Пример: четырёхугольник ABCD

До декомпозиции:

Узел: (1, square)
Связь: ("ABCD", 1, isSignOf)

После декомпозиции:

4 узла точек: (2, point), (3, point), (4, point), (5, point)
4 обозначения: ("A", 2, isSignOf), ("B", 3, isSignOf), ("C", 4, isSignOf), ("D", 5, isSignOf)
4 стороны (отрезки): (6, piece), (7, piece), (8, piece), (9, piece)
Связи принадлежности точек четырёхугольнику
Связи "является вершиной отрезка" для каждой стороны

Этап 2: Унификация (объединение одинаковых)

Если встречаются понятия с одинаковыми обозначениями — они объединяются.

Пример: треугольник ABC и отрезок AB

До унификации:

Треугольник ABC → точки A₁, B₁, C
Отрезок AB → точки A₂, B₂

После унификации:

Точка A (общая для треугольника и отрезка)
Точка B (общая)
Точка C (только треугольника)
Отрезок AB — это сторона треугольника!

Этап 3: Очистка (удаление лишнего)

Удаляются узлы, которые были созданы на этапе декомпозиции, но не участвовали в унификации — они избыточны.

Классы геометрических фигур

Каждая фигура — это класс, реализующий интерфейс IFigure с методом draw().

Реализованные классы фигур

Point — точка
Line — прямая
Ray — луч
Piece — отрезок
Triangle — треугольник
Square — четырёхугольник
Circle — окружность
Perpendicular — перпендикуляр
Parallel — параллельная прямая
Median — медиана
Bisectrix — биссектриса
MiddlePerpendicular — срединный перпендикуляр
Corner — угол

Конструкторы фигур

Ключевая идея: одна фигура может быть задана разными способами. Каждый способ — отдельный конструктор.

Класс Circle — три конструктора

1. По центру и радиусу:

Circle(Point center, double radius)

2. По центру и точке на окружности:

Circle(Point center, Point pointOnCircle)

3. По трём точкам на окружности:

Circle(Point p1, Point p2, Point p3)

Все три способа однозначно определяют окружность! Программа выбирает конструктор в зависимости от доступных данных.

Класс Triangle — два конструктора

1. По трём вершинам:

Triangle(Point a, Point b, Point c)

2. По двум вершинам и углу:

Triangle(Point a, Point b, Angle angle)

Алгоритм рисования: псевдокод

Основной цикл построения

while (не все фигуры нарисованы) {
    
    // Ищем фигуры, для которых есть все опорные точки
    for (каждая ненарисованная фигура F) {
        constructor = найтиПодходящийКонструктор(F);
        if (constructor && всеОпорныеТочкиЗаданы(constructor)) {
            нарисоватьФигуру(F, constructor);
            continue;
        }
    }
    
    // Ищем точки, однозначно заданные нарисованными фигурами
    for (каждая ненарисованная точка P) {
        if (P.принадлежитНарисованнойФигуре() && 
            P.положениеОднозначноЗадано()) {
            нарисоватьТочку(P);
            continue;
        }
    }
    
    // Если прогресс застопорился — рисуем случайную точку
    if (нетПрогресса) {
        P = найтиТочкуСМинимальнойСтепеньюСвободы();
        нарисоватьТочкуСлучайно(P);
    }
}

Степени свободы точки

Когда точка не задана однозначно, программа вычисляет её степень свободы — количество независимых параметров.

Классификация по степеням свободы

0 степеней — точка задана однозначно:

Пересечение двух прямых
Центр заданной окружности
Середина заданного отрезка

1 степень — точка на линии:

Точка на прямой (параметр: расстояние вдоль прямой)
Точка на окружности (параметр: угол)
Точка на отрезке (параметр: позиция от 0 до 1)

2 степени — свободная точка:

Произвольная точка на плоскости (параметры: x, y)

Выбираем точку с минимальной степенью свободы — так результат меньше зависит от случайности.

Структура проекта (Java пакеты)

Модульная архитектура

Пакет geom — геометрические примитивы:

Классы фигур с методами draw()
Генераторы случайных фигур
Вычисления координат опорных точек

Пакет semantic — ядро логики:

Word — слово в тексте
AbstractNode — узел сети
AbstractLink — связь в сети
SemanticAnalyzer — построение сети из текста
NetworkNormalizer — декомпозиция/унификация
PictureBuilder — алгоритм рисования

Подпакет semantic.nodes — типы узлов:

SignNode — обозначение
PointNode — точка
LineNode — прямая
TriangleNode — треугольник
и т.д.

Подпакет semantic.links — типы связей:

IsSignOfLink — отношение обозначения
BelongLink — принадлежность
IsVertexLink — "является вершиной"
PerpendicularLink — перпендикулярность
и т.д.

Пакет gui — интерфейс (Swing):

Текстовое поле для ввода условия
Кнопки управления
Canvas для отрисовки результата
Визуализация семантической сети (через GraphViz)

Практики программирования

Проект использовал принципы, которые обеспечили чистоту и расширяемость кода:

Инкапсуляция: каждая фигура "умеет себя рисовать" — метод draw()
Полиморфизм: все фигуры реализуют общий интерфейс IFigure
Разделение ответственности: анализ текста, обработка сети, рисование — отдельные модули
Открытость расширению: чтобы добавить новую фигуру, достаточно реализовать IFigure
Тестируемость: каждый модуль можно тестировать независимо

Использование программы

Рабочий процесс:

Пользователь вводит текст задачи в текстовое поле
Нажимает кнопку "Построить"
Программа показывает промежуточные результаты:
- Семантическую сеть (граф) — для отладки
- Нормализованную сеть
Отрисовывается финальная иллюстрация
В случае ошибки — показывается, на каком этапе возникла проблема

Интеграция с GraphViz

Для визуализации семантической сети использовалась библиотека GraphViz:

Программа генерирует .dot файл (текстовое описание графа)
GraphViz рендерит его в изображение
Изображение отображается в GUI

Это позволяло видеть, как программа понимает текст — бесценно для отладки!

Ограничения реализации

Что не было реализовано (и почему это интересно):

Местоимения: "его диагональ", "её центр" — требует анализа контекста и кореферентности
Неоднозначности: "высота треугольника" — какая из трёх? Нужна эвристика выбора
Вложенные определения: "в треугольнике, образованном…" — сложная грамматика
Неявные построения: "точка пересечения медиан" — нужно сначала построить медианы
Метрические ограничения: "отрезок длиной 5 см" — нужна система единиц и масштаб

Каждое ограничение — это отдельное исследование! Проект показал принципиальную возможность, но до «промышленной» системы ещё далеко.

Расширение на другие языки

Архитектура спроектирована с учётом мультиязычности:

Шаблоны хранятся отдельно от кода
Чтобы поддержать английский — достаточно написать новые шаблоны
Геометрическая логика (модули geom, semantic) не зависит от языка

Пример шаблона для английского:

English template: LABELING

<geometric_object> <label>

Matches: "triangle ABC", "segment MH", "point X"

Философское отступление

Язык описывает мир, но геометрия показывает его. Перевод между ними — это не просто техническая задача, а моделирование того, как разум связывает символы с образами.

Проект исследует фундаментальный вопрос: как мы думаем о пространстве?

Когда вы читаете «биссектриса угла», в голове не возникают слова — возникает картинка. Зрительные образы — язык творческого мышления. Психологи утверждают: человек не может помыслить понятие, не визуализировав его.

Заставляя компьютер превращать текст в рисунок, мы:

Формализуем неявные процессы человеческого мышления
Проверяем гипотезы о том, как устроено визуальное мышление
Создаём инструменты, которые усиливают наши когнитивные способности

Ограничения и будущее

Что не работало (тогда)

Местоимения («её диагональ пересекла…») — нужен анализ контекста
Сложные вложенные конструкции
Неоднозначности естественного языка
Ограниченный набор фигур и связей

Направления развития

Интеграция с LLM для лучшего понимания текста
Расширение на стереометрию (3D геометрия)
Интерактивность: пользователь может корректировать картинку, уточняя понимание
Мультиязычность: работа не только с русским
Обратная задача: по картинке генерировать текстовое описание

Выводы

Автоматическое построение иллюстраций к геометрическим задачам — это больше, чем просто «удобная фича» для учебников. Это:

Исследование природы визуального мышления
Практика формализации «очевидных» процессов
Демонстрация того, что даже узкая задача (планиметрия) полна нетривиальных вызовов
Пример того, как правильно выбранные абстракции (семантические сети, классы фигур, конструкторы) делают сложное решаемым

«Моделирование умственной деятельности человека при построении геометрического изображения вполне реалистично» — но требует глубокого понимания того, как мы думаем о пространстве.

Проект 2009 года заложил фундамент. Современные технологии могут построить на нём небоскрёб. Но принципы — извлечение смысла, моделирование зависимостей, уважение к геометрической логике — останутся неизменными.

Техническая реализация: Java, Swing (GUI), собственный язык шаблонов для NLP, семантические сети на основе графов. Исходный код включал модули geom (геометрические примитивы), semantic (анализ и сеть), gui (интерфейс).

О дипломе: Работа защищена в 2009 году в Академическом физико-технологическом университете РАН (Санкт-Петербург). Научный руководитель — д.ф.-м.н., доцент А.В. Омельченко. Рецензент — к.ф.-м.н., доцент С.И. Николенко.

← Вернуться на главную